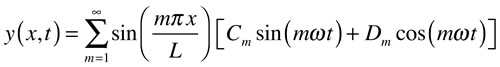
*
[Note: The Java Applet for this animation can no longer be run in a web browser. Clicking this link, however, will download to your computer a Java Web Start file named StringLaunch.jnlp. This file can launch the animation in a separate window on your computer. Downloading and executing the file may be blocked by local Java permissions, but persevere! You may finally have to launch the file by right-clicking (control-clicking) it and choosing Open, instead of simply double-clicking it.]
*
This animation shows in slow motion the transverse motion of an ideal string of length L, fixed at both ends, that has been bowed, plucked, or hit by a hammer. A typical string of musical interest goes through hundreds of these cycles each second. In each example, one can choose the point along the string where the excitation is applied. In addition, one can select another point along the string, label it with a red dot, and plot the position of that point as a function of time.
Since evidence for the classical Helmholtz motion of a bowed string is often given by measuring the transverse velocity of a point on the string, a graph of that velocity is also available for the bowed string.
A special feature of the bowed string case is a portrayal of the stick-slip bowing mechanism. The ladder-like object on the left side of the string is a representation of a violin bow moving upward at constant velocity. When the yellow dot is showing on the bow, the string and the bow are stuck together at that point; for typical bowing positions this is the situation for much more than half of each cycle. When the traveling kink in the string arrives at the bow, it detaches the string from the bow and the string slips under reduced friction to a new place lower on the bow. There it sticks again and the bow pushes the string upward again at constant velocity.
Another graph provided is the transverse force exerted on the left-hand support by the string as a function of time. This is calculated in a small-angle approximation assuming that the tension in the string is constant, and that the transverse component of the tension is proportional to the slope of the string.
The motions are computed from sums of normal mode motions, using appropriate relative amplitudes and phases in each case. Expressions for the sums are given below in the section titled “Technical Details.” Because the sums were terminated after 40 terms, some wiggles are still present in graphs, especially at discontinuities where the Gibbs phenomenon is evident.
1. At the bottom of the window are several controls for the display. On the left is a slider which can be used to move the excitation point to any location on the left half of the string. Next to that is a button labeled “Go/Stop.” Clicking the button at any time stops or restarts the motion.
The remaining controls at the bottom of the window are only effective when a graph has been chosen from the menu. The button labeled “Clear” restarts the graphing if desired when system changes in mid-graph have modified the character of the graph. The right-hand slider may be used to move the point whose motion is being graphed to any location on the right half of the string.
2. At the top of the window is a menu bar that affects the display. Available menu choices and their effects are the following:
| Menu Choice | Action |
|---|---|
| Strings > About Strings | Reveals the name of the author and the year the applet was written. |
| Excitation > Bowed | Selecting this shows the motion of a bowed string. The location of the bow may be changed using the left-hand slider at the bottom of the window, but the motion of the string does not depend on this location. Only the speed of the bow changes. |
| Excitation > Plucked | Selecting this shows the motion of a plucked string. When this entry is first chosen the initial fixed shape of the string is shown, and the motion must be started using the “Go/Stop” button at the bottom of the window. The cross indicates the location of the plucking point, which may be moved using the left-hand slider at the bottom of the window. |
| Excitation > Hammered | Selecting this shows the motion of a string struck with a hammer. When this item is first chosen the string is shown as a straight line, with an arrow showing where the hammer will strike the string when the “Go/Stop” button is clicked. The striking point may be adjusted by the left-hand slider at the bottom of the window. |
| Graph > Displacement | Selecting this turns on or off a graph of the transverse position of the observation point as a function of time. The observation point is shown by a red dot on the string and may be moved using the right-hand slider. This graph and the other graphs may be displayed simultaneously. |
| Graph > Force | Shows or blanks a graph of the transverse force of the string on the left support as a function of time. This and the other graphs may be displayed simultaneously. |
| Graph > Velocity | Toggles a graph of the transverse velocity of the observation point on only the bowed string as a function of time. This and the other graphs may be displayed simultaneously. |
Any possible vibration of a linear mechanical system may be expressed as a sum of its normal mode motions, using appropriate relative amplitudes and phases. In a pure normal mode motion, each part of the system moves with simple harmonic motion at the same frequency, and all parts pass through their equilibrium positions simultaneously. Each mode is characterized by its shape, frequency, and damping time. The actual vibration of a string in any real instrument must be expressed as a sum of its normal modes rather than a single, pure normal mode motion .
In the case of an ideal string of length L fixed at both ends, the normal modes of transverse motion are sinusoidal curves with wavelength such that there are zeros at each end of the string. It turns out that the frequencies of mode vibrations of a string are integer multiples of the lowest mode frequency. This guarantees that arbitrary sums of mode vibrations will yield periodic disturbances and hence that vibrating strings will be basic components of many musical instruments.
A mathematical expression for the general transverse motion of an ideal string, expressed as a sum of its normal modes may be written
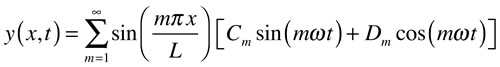
where
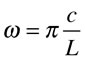
The x-dependent part contains the shape of each mode, and the time-dependent parts yield the motion. The two constants in each term allow one to adjust the amplitude and phase of each mode in the sum. In the expression for the fundamental angular frequency, c is the speed of propagation of a transverse wave on the string.
If one takes for initial conditions that each point has zero transverse velocity, and an initial triangular shape with a vertex at x = d and a distance A from the axis, the two constants in the sum may be evaluated. The resulting sum, used to create the animation, is
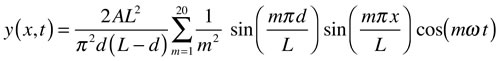
If one takes for initial conditions that each point has zero displacement, and velocity given by a Dirac delta function at x = d, the two constants in the sum may be evaluated. The resulting sum, used to create the animation, is
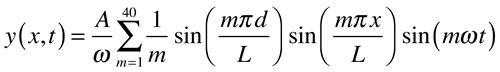
The sum used to create the animation is
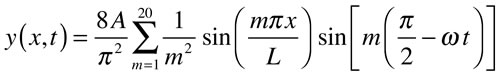
While different from the initial conditions used to evaluate the constants here, a simpler set ought to be an initial displacement of zero, and an initial velocity that is zero at the left end of the string and increases linearly with distance from the left end.
The sums given here for the plucked and hammered strings, and the resulting motions shown in the animation are reasonable for the initial motions of a string disturbed and then let vibrate. But since the damping time for high frequency modes is typically shorter than the damping time for low frequency modes, the amplitudes of the high-frequency modes decrease with internal friction more rapidly than those of the low frequency modes. If the string is left to vibrate on its own, the character of the sum gradually changes. The higher terms in the sum slowly go away, and eventually the string approaches a vibration in only its lowest frequency or fundamental mode.
An indication of how the first few normal modes of the string add up to the plucked and bowed motions is given in another animation in this series titled “String Modes.”