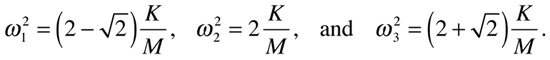
*
[Note: The Java Applet for this animation can no longer be run in a web browser. Clicking this link, however, will download to your computer a Java Web Start file named ThreeDegreesLaunch.jnlp. This file can launch the animation in a separate window on your computer. Downloading and executing the file may be blocked by local Java permissions, but persevere! You may finally have to launch the file by right-clicking (control-clicking) it and choosing Open, instead of simply double-clicking it.]
*
This animation shows the vibrations of a system of three equal masses, joined to each other and fixed terminations by four identical springs. Since it takes three variables to specify the location of all the masses at any time, this system is said to have three degrees of freedom. It follows from theorems of classical mechanics that the system possesses only three distinct normal modes of vibration.
There are two basic sets of displays in the animation. The first set, under way when the applet is launched, shows the normal modes of vibration of the system. Any of the three different modes may be chosen from the Action menu, where they are listed in order of increasing frequency. As the masses move, graphical histories of their positions may be drawn on axes extending below the masses.
The frequency of a normal mode depends on the mass of each object and the force constant of each spring. Here the frequency of each mode is expressed as a multiple of the lowest-freqency mode. The frequencies of the higher modes are clearly not integer multiples of the lowest mode frequency, and hence motions obtained by combining several modes will not be periodic.
The second set of displays shows motions of the system with either of two specific initial conditions. The motions are computed from sums of the normal mode motions, using appropriate relative amplitudes and phases in each case. Expressions for the sums are given below in the section titled "Technical Details." Since the motion is not periodic, it is followed for about 45 seconds and then the animation stops. It may be repeated by selecting it again from the Action menu.
1. At the bottom of the display are two buttons which control the display. Clicking the button labeled "Go/Stop" at any time starts or stops the motion. The button labeled "Graphs " toggles the presentation of all the tracks for the time history of the masses' motions.
2. At the top of the window is a menu bar that affects the display. Available menu choices and their effects are the following:
| Menu Choice | Action |
|---|---|
3 Degrees > About 3 Degrees |
Reveals the name of the author and the year the applet was written. |
Action> (5 choices) |
Selecting an item from this menu causes the display to show the chosen normal mode motion, or the motion following two specific initial conditions. |
Any possible vibration of a linear mechanical system may be expressed as a sum of its normal mode motions, using appropriate relative amplitudes and phases. In a pure normal mode motion, each part of the system moves with simple harmonic motion at the same frequency, and all parts pass through their equilibrium positions simultaneously. Each mode is characterized by its shape, frequency, and damping time. For a general initial condition, the actual motions of the system must be expressed as a sum of its normal modes rather than as a single, pure normal mode motion. Only if the frequencies of the normal mode vibrations are integer multiples of a lowest frequency will the general motion be periodic.
Upon solving the coupled equations for the three-mass four-spring system, assuming a form with sinusoidal time dependence, one finds that solutions exist only for three different angular frequencies whose squares are
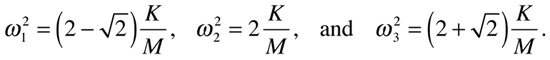
Here, K is the spring constant of each spring, and M is the mass of each block.
Denoting the three masses by the letters A, B, and C, respectively, the normal mode displacements associated with these three frequencies are
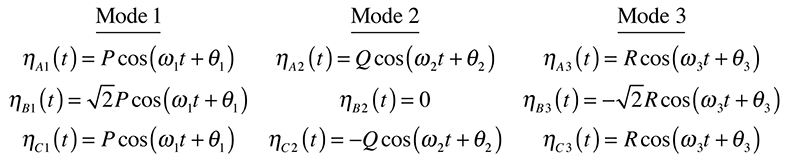
where the θ’s are phase constants, and P, Q, and R, are arbitrary constants that set the amplitude of each mode.
The general motion of any mass in this system with three degrees of freedom may always be expressed in terms of the three normal mode motions:
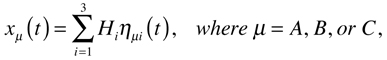
where the coefficients Hi are evaluated from initial conditions. For example, if all the masses are initially at rest and mass A has an initial displacement of D while masses B and C are initially in their equilibrium positions, then
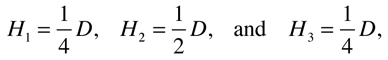
where P, Q, and R have all been set equal to 1, and the phase constants are zero. Similarly, if all the masses are initially at rest, mass A has an initial displacement of D, mass B has an initial displacement of 2/3 D, and mass C has an initial displacement of 1/3 D, then
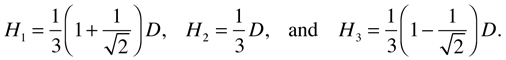
(With P = Q = R = 1 and zero phase constants.)