| Mechanics > Work
and Energy > Conservation of Energy |
DCS# 1M40.20 |
LOOP THE LOOP
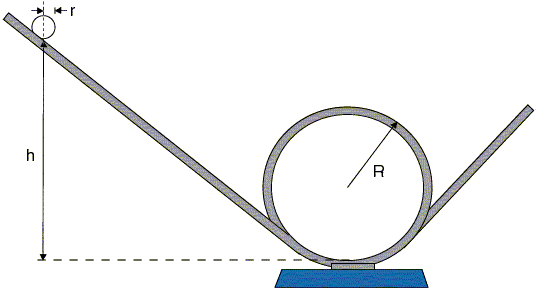
-
APPARATUS
| loop the loop track |
202-13-F |
| plastic ball |
202-14-E5 |
| meter stick |
101-05-F |
ringstand
and clamp
|
202-01
|
DESCRIPTION
Calculate
the
minimum height from which the ball must be released in order to
make it through loop and then verify this experimentally.
NOTES
Brace the track so energy is not
lost to its wobbling.
potential energy at initial height = translational + rotational
+ potential energy at top of loop
mgh = 1/2 Iω2 + 1/2 mv2
+ 2mg(R-r)
- substitute:
- I = 2/5 mr2 for a
solid sphere
ω= v/r, assuming ball makes contact
with bottom rather than edges of track
v2 = g(R-r) since gravity
provides centripetal force at the top of the loop
h = 2.7(R-r)

