Sediment Transport - Monday: February 16, 2004
I’ve asked you to do two sets of simple calculations for class Monday using sites on the web.
FALL VELOCITY (go to :http://www.wes.army.mil/el/dots/doer/subtools/dtb010.html)
This site computes fall velocity, which is defined as the rate at which
spherical grains of a given size and density will fall through water. (Hint:
you might want to print this page out first for reference while you navigate
the exercise - and then add it to your notes).
After looking over the web page for general background, click on "Input" to enter numbers for your calculations.
Once you fill in several variables, the page will calculate fall velocity
for you. Let’s assume quartz, which has a specific gravity of
2.65 g/cm3. Remember what that is? For the calculations,
- Set current velocity at 0.
- Water Depth and Draft (the depth at which the sediment will be dumped into
the water by the dredge) are not pertinent to this exercise; they are used to
determine how far the grains will travel before hitting the bottom. Use 10m
for depth and 5 m for draft just to fill in all the boxes.
- Keep water temperature at 25°C.
Do the calculations for the following grain sizes. Then GRAPH
fall velocity (x axis) versus sediment size (y-axis). If you use Excel, it’s
really quick:
Median Grain Size
0.1mm
0.3 mm
0.5 mm
1 mm
1.5 mm
2 mm
2.5 mm
3 mm
3.5 mm
4 mm
Questions (before class, please):
1. How will fall velocity relate to the erodability of a sedimentary bottom with these median grain sizes?
2. Why?
3. Why should we care?
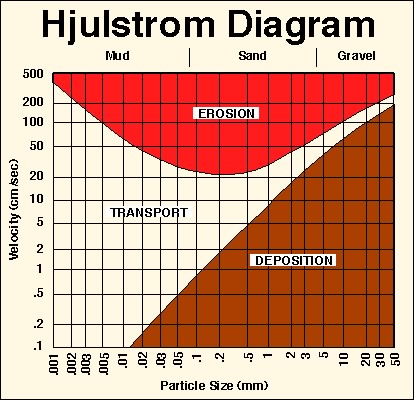
Now, look at the diagram below. It describes the erodability of sediments of different sizes. There is another much more accurate graph that relates something called shear velocity to erodability. I have chosen to stay with the Hjulstrom Diagram as the idea of velocity is an easier one to grasp.
Current velocity is given on the left. Grain size (in mm) is along the bottom (increases to the right). The red area is the current that needs to be reached to get a grain of a given size off the bottom (to erode). The brown curve is the velocity at which grains of a given size will fall out of the curent and be deposited.

Questions:
1. Generally, how does sediment size relate to its stability on the bottom?
2. How does this relate to the Fall Velocity curve you created above?
3. Why is there a "gap" between the erosion and transport curves (i.e., why doesn't a grain erode and deposit at the same velocity)?
4. Why does the velocity needed to erode a grain increase for both large and very small grains?
SEDIMENT TRANSPORT (go to: http://www.coastal.udel.edu/faculty/rad/sand.html):
This page will compute how fast sediment will be moved by waves of a given height
and approach angle to the beach. If you are interested in the general formula,
it is provided below on the page. Transport volume will generally be related
to the longshore component of wave energy and the settling velocity of a “typical”
beach grain.
You will input the following values:
- Breaker height: use: 0.1, 0.3, 0.5, 1.0, 2.0, 4.0 and 8.0 m
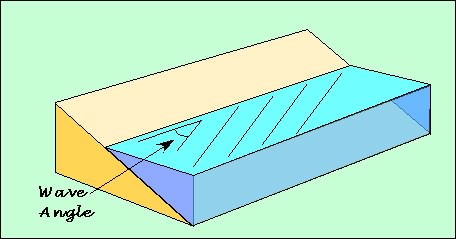
- Breaker Angle: this is the angle between the beach and the
breaking wave crest. Keep it at 10.0°
- K is a “computational constant, i.e., a “fudge
factor”, that takes into account turbulence and the ratio between water
and sediment.
- Set Berm Height (the elevation of the top of the beach) at
2.0 m
- Leave Depth of Closure at 6m (this is basically a point where
uprushing water meets outgoing return flow; we’ll talk about it later
in the course)
GRAPH this relationship (again, EXCEL is quickest; just put the heights in the first column and copy the output results into the second column).
Questions:
1. How does height affect the volume of sediment that a wave will move?
2. Why?
3. What factor do they seem to have left out here?
4. Why might this be OK?
NOW, we are going to set wave height at 1 m and vary the angle at which the waves breaks relative to the shoreline trend. Keep the other setting the same as above.
Compute AND GRAPH the volume of sediment that will be transported for the following wave angles: 1, 5, 10, 20. 30, 45, 50, 60, 70, 90°.
Questions:
1. What happens to the volume of material that is transported by a wave as you change the angle of approach relative to the beach?
2. What happens at 45°? Why?